In computer science, a tree is a widely used abstract data type (ADT) that simulates a hierarchical tree structure, with a root value and subtrees of children with a parent node, represented as a set of linked nodes.

There are many basic data structures that can be used to solve application problems. Array is a good static data structure that can be accessed randomly and is fairly easy to implement. Linked Lists on the other hand is dynamic and is ideal for application that requires frequent operations such as add, delete, and update. One drawback of linked list is that data access is sequential. Then there are other specialized data structures like, stacks and queues that allows us to solve complicated problems (eg: Maze traversal) using these restricted data structures. One other data structure is the hash table that allows users to program applications that require frequent search and updates. They can be done in O(1) in a hash table.

One of the disadvantages of using an array or linked list to store data is the time necessary to search for an item. Since both the arrays and Linked Lists are linear structures the time required to search a “linear” list is proportional to the size of the data set. For example, if the size of the data set is n, then the number of comparisons needed to find (or not find) an item may be as bad as some multiple of n. So imagine doing the search on a linked list (or array) with n = 106 nodes. Even on a machine that can do million comparisons per second, searching for m items will take roughly m seconds. This not acceptable in today’s world where speed at which we complete operations is extremely important. Time is money. Therefore it seems that better (more efficient) data structures are needed to store and search data.

In this chapter, we can extend the concept of linked data structure (linked list, stack, queue) to a structure that may have multiple relations among its nodes. Such a structure is called a tree. A tree is a collection of nodes connected by directed (or undirected) edges. A tree is a nonlinear data structure, compared to arrays, linked lists, stacks and queues which are linear data structures. A tree can be empty with no nodes or a tree is a structure consisting of one node called the root and zero or one or more subtrees. A tree has following general properties:

• One node is distinguished as a root;
• Every node (exclude a root) is connected by a directed edge from exactly one other node; A direction is: parent -> children
  

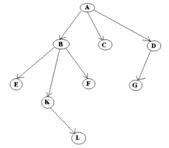
A is a parent of B, C, D,
B is called a child of A.
on the other hand, B is a parent of E, F, K

In the above picture, the root has 3 subtrees.

Each node can have arbitrary number of children. Nodes with no children are called leaves, or external nodes. In the above picture, C, E, F, L, G are leaves. Nodes, which are not leaves, are called internal nodes. Internal nodes have at least one child.

Nodes with the same parent are called siblings. In the picture, B, C, D are called siblings. The depth of a node is the number of edges from the root to the node. The depth of K is 2. The height of a node is the number of edges from the node to the deepest leaf. The height of B is 2. The height of a tree is a height of a root.